볼트 설계법과 그 계산 방법은 ? (사이즈 및 강도구분 결정)
머릿말
우선 한 쌍의 볼트와 너트를 중공원통 피체결부재에 체결 후 중공원통 체결체에 외력이 작용했을 때 볼트에서 발생하는 축력의 변화(내력 계수)를 추정하기 위하여 볼트의 용수철 정수 및 피체결체의 용수철 정수 등의 기초 계산을 해야 할 필요가 있으며, 계산의 간편화를 위하여 내력 계수를 같은 재질의 경우 0.1, 2쌍의 피체결체중 한 쌍만 다른 재질인 경우 0.15, 두 쌍 다 다른 재질일 경우 0.2로 계산하였습니다.
볼트 너트 피체결체 모두 탄소강 재질일 경우 실험상 내력 계수가 높지 않았던 결과를 토대로 0.1의 수치로 계산하였습니다.
나사 체결체의 설계 개념
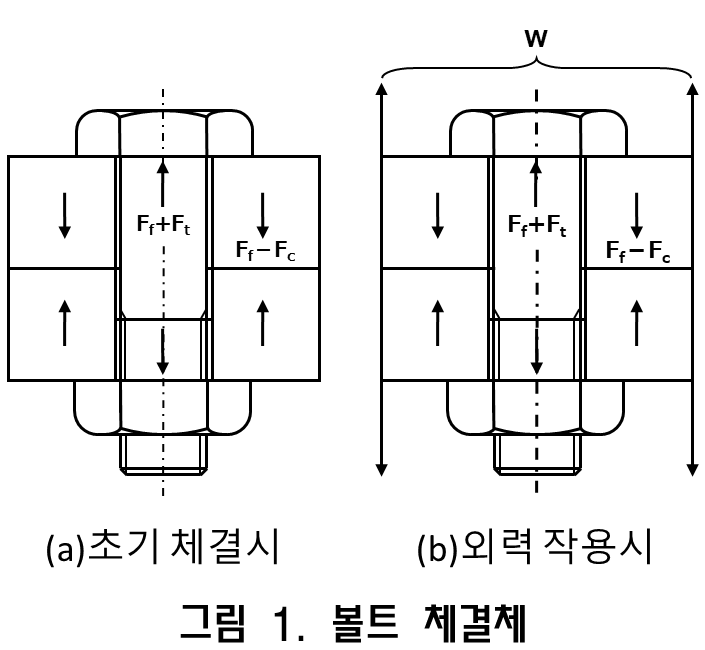

그림 1과 같이 2개의 중공원통을 한 쌍의 볼트와 너트로 체결 한 볼트 체결체의 볼트로 어떤 설계를 할지 생각해 봅시다.
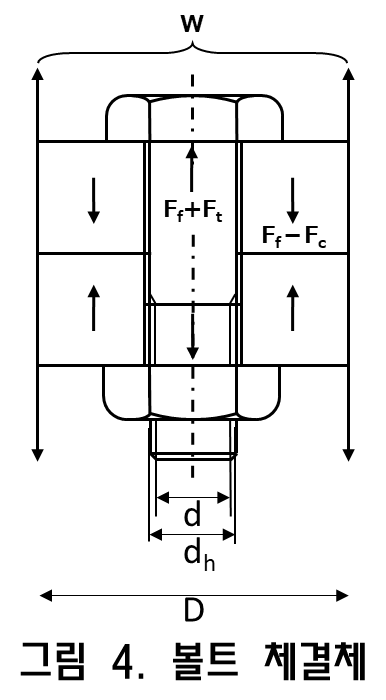
볼트 체결체는 처음에 초기 축력 Ff로 체결됩니다. 이 상태에서는 그림 1과 같이 일반적으로 축 방향으로 인장하는 하중(외력) W 혹은 축 직각 방향의 전단응력 Q가 작용하는 경우가 많습니다. 여기서는 축 직각 방향 하중 W가 적용되는 경우에 대하여 이야기하겠습니다. 하중이 가해지면 볼트에는 인장력이 증가하여 Ft가 추가되며 2개의 중공원통(이하 피체결체라고 부름)의 접합면에서는 Fc의 힘이 감소합니다. 즉 볼트 축력은 Ff + Ft가 되며 접합면의 체결력은 Ff – Fc가 됩니다. 힘의 균형에서 다음 식 (1-1)이 주어집니다.
| 식 (1 – 1) – – – – – 식 (1 – 1) | 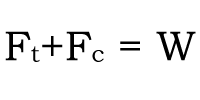 |
Ft와 Fc가 미지수 이므로 주어진 방정식은 하나로써 이 문제는 이대로는 풀 수 없습니다.
즉, 해당 식은 부정합 문제입니다. 해당 식은 역사적으로 1938년 독일에서 출판한 책에 처음으로 푸는 방법이 소개되어, 현재에 이르러서는 일본 기계 설계의 책에서 소개되고 있습니다. 해당 식은 외력이 작용할 때 Ft값이 어느 정도가 될지 예상하는 것이 과제입니다. 여기서Ft / W의 값을 내력 계수라고 부르며 일반적으로 다음과 같은 식으로 나타냅니다.
| 식 (1 – 2) – – – – – 식 (1 – 2) | 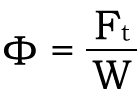 |
Φ의 값을 정하면 식 (1-1)과 같이 Fc의 값은 다음 식과 같이 주어집니다.
| 식 (1 – 3) – – – – – 식 (1 – 3) | 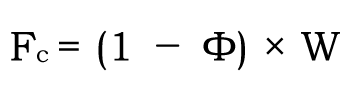 |
여기서 이와 같이 볼트 체결체(체결체란 볼트 너트가 부재에 피체결된 상태)를 설계함에 있어서 예전 독일 융커씨는 아래의 4가지를 조건을 고려하는 것이 중요하다고 지적하였습니다. 또한 본 설계법에서는 접합면에 잔류하는 힘(응력)을 중시하여 추가하였습니다.
4가지 조건
1) 반복 하중(W 혹은 Q가 기계작동 중에 몇 번이나 반복해서 작용하는가)에 대하여 볼트(나사)가 풀리지 않을 것.
2) 외하중(W 혹은 Q)의 작용에 대하여 볼트에 생기는 최대 응력이 볼트 재료의 항복 응력을 넘지 않을 것 (일부러 볼트의 항복 응력이 되도록 체결하는 방법도 있지만 여기서는 기본적인 토크 방법을 채용)
3) 반복 외 하중에 대하여 볼트가 피로 파괴하지 않을 것
4) 볼트 체결체의 기능을 수행하기 위하여 필요한 접합면 응력이 확보될 것.
위의 4가지 조건을 만족시키기 위하여 어떤 볼트로 설계할지, 즉 볼트의 유효경(호칭 사이즈)과 강도구분(볼트의 강도)을 선택할지가 문제입니다. 게다가 볼트 초기 축력 Ff을 정하고 값을 얻기 위해 볼트와 너트 체결 토크 T가 필요합니다.
조건 1)에 대한 설계 방침
외력 작용에 의한 풀림의 발생 방지를 위하여 VDI2230에 따른 고강도 볼트에 대해서는 초기 축력 Ff를 체결에 따른 전단 응력을 포함한 미제스 상당응력이 볼트의 항복 응력(내력)의 90%이하에 가능한 크게 설정합니다. 수나사의 체결에 따라 발생하는 전단응력 τ는 식 (1-4)과 같습니다.
| 식 (1 – 4) – – – – – 식 (1 – 4) | 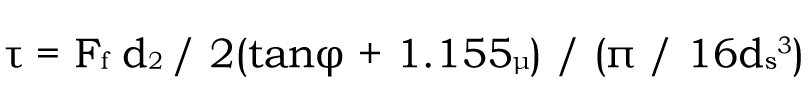 |
여기서 φ : 나사의 리드각, ds : 유효 단면과 같은 원의 지름, μ : 마찰계수, d2 : 수나사의 유효경 기본 수치
식 (1-4)과 초기 축력 (Ff)max에 따른 응력 σfmax( = (Ff)max / As)을 이용하면 미제스 응력 σv는 아래 식 (1-5)와 같습니다.
| 식 (1 – 5) – – – – – 식 (1 – 5) |  |
즉,
| 식 (1 – 6) – – – – – 식 (1 – 6) | 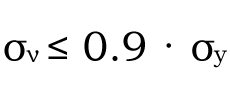 |
여기서 σy는 볼트 재료 항복 응력, As는 유효 단면적입니다.
게다가 외력이 작용할 때 접합면에 잔류하는 체결력 Fkerf를 지정합니다
조건 2)에 대한 설계 방침
축 방향 외력(하중) W가 작용하면, 볼트 축력은 최대 Ff + Ft가 됩니다. 볼트가 파손(항복 응력을 초과)될 때, 볼트의 나사부와 너트의 나사부 간의 맞물림이 좌면의 제1나사 골짜기에 응력이 최대가 되는 것으로 알고 있습니다.
따라서 관행으로는 위의 최대 힘을 나사 유효 단면적에서 뺀 값(응력)이 항복 응력 이하가 되도록 Ff를 결정하게 됩니다. 그러나 볼트를 체결할 때 볼트 축 비틀림에 의해 전단 응력이 발생하기 때문에 이 전단 응력을 고려할 필요가 있습니다.
볼트의 응력이 파손 응력(항복 응력 혹은 내력)을 초과하지 않게 하기 위해서는 아래 식 (1-7)으로 확인할 필요가 있습니다.
| 식 (1 – 7) – – – – – 식 (1 – 7) | 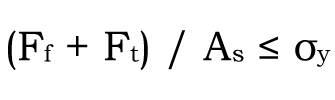 |
※위 식에서 Ft의 값은 식 (1-1)에서 구하였습니다.
그러나 실제 볼트 체결력은 편차가 있어 어떻게 정할지가 문제입니다.
일반적으로 가스켓 등을 삽입하지 않는 그림 1에 나타난 볼트 체결체 등에서는 예외(커넷팅 로드 볼트)를 제외하고, 축 방향 외력 W가 작용할 때의 볼트 축력의 증가분 Ft는 0.1W이하로 설정합니다.
조건 3)에 대한 설계 방침
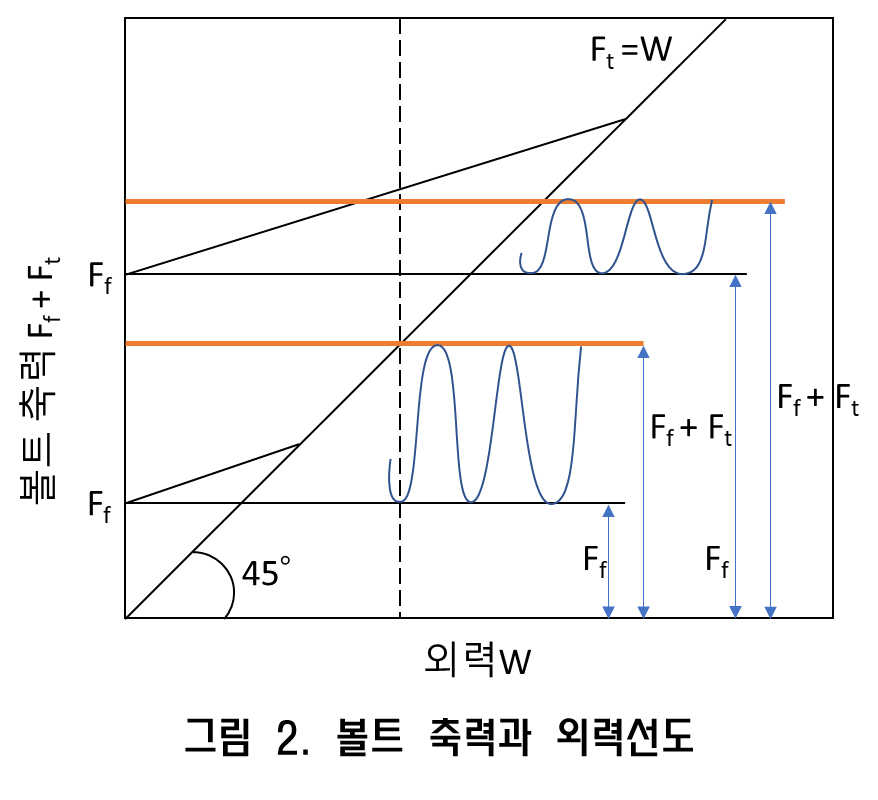
피로로 볼트가 파괴되는 이론으로는 수나사 좌면 측 제1나사 골짜기입니다. 아래의 그림 2에서 나타나듯이 외력 W가 0 ~ W까지 작용할 때, 볼트 축력의 변동은Ff ~ Ff + Ft입니다. 그림 2는 볼트 초기 축력 Ff로 체결한 체결체에 외력 W가 작용되면 볼트 축력이 Ff + Ft가 되는 것이 확인 가능합니다. Ft는 최초 W의 증가에 대하여 직선적으로 증가하며, 이윽고 접합면이 분리되면 곡선선상으로 증가합니다.
접합면이 완전히 분리되면 Ft = W가 되며 45°기울기의 직선이 됩니다. Ff가 보다 작으면 외력 W0의 수치에 대하여, 접합면이 분리되기 때문에 Ft의 수치가 커집니다. Ff가 보다 커지면 같은 크기의 W0가 작용해도 Ft의 값은 보다 작아지는 것을 나타냅니다.
일반적으로 나사 골짜기 단면적 Ar을 사용하기 때문에 볼트 응력의 변동은 (Ff + Ft) / Ar ~ Ff / Ar입니다. 이러면 응력 진폭은 다음과 같은 식 (1-8)이 되고 이것을 볼트 재료의 피로 한도 σa이하로 할 필요가 있습니다.
| 식 (1 – 8) – – – – – 식 (1 – 8) | 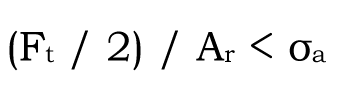 |
접촉 응력 σm은 σm = (Ff + Ft / 2) / Ar가 됩니다.

조건 4)에 대한 설계 방침
외력이 작용하면 피체결물의 접합면(접합면의 단면적을Ai라고 한다.) 응력은 아래와 같습니다.
| 식 (1 – 9) – – – – – 식 (1 – 9) | 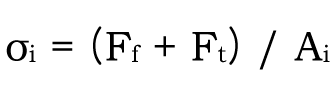 |
이것이 필요한 응력 σreq이상으로 확보할 필요가 있습니다. 그렇지 않으면 예를 들어 비틀림 하중이 작용될 때 접합면이 미끄러져 회전해버립니다. 회전하지 않도록 접합면 응력이 필요합니다. 게다가 가스켓을 넣는 밀봉성(누설되지 않도록)을 필요로 할 경우도 같습니다.
따라서 아래의 식 (1-10)을 만족해야 합니다
| 식 (1 – 10) – – – – 식 (1 – 10) | 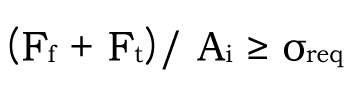 |
이상 설계의 기본 방침에 대하여 설명했습니다만, 결국 어떻게 해야 좋을지 처음 말했듯이 외력 W가 작용할 때 볼트에 발생하는 축력의 증가분 Ft와 접합면에서 잃는 힘Fc를 설계 단계에서 보다 정확하게 추정할 필요가 있다고 알게 되었습니다.
볼트 용수철 정수 Kt , 피체결체의 압축 용수철 정수Kc로 할 때 식 (1-1)의 방정식을 만족하는 조건이면 외력 W가 작용할 때의 볼트 좌면의 볼트 인장과 피체결부재의 인장이 같은 조건에서 Ft와 Fc는 용수철 정수 Kt와 Kc를 이용한 Thum&Debus는 아래의 식 (1-11)을 제안합니다.
| 식 (1 – 11) – – – – 식 (1 – 11) | 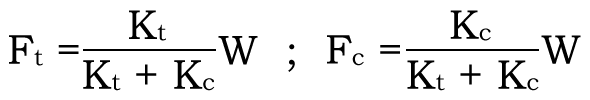 |
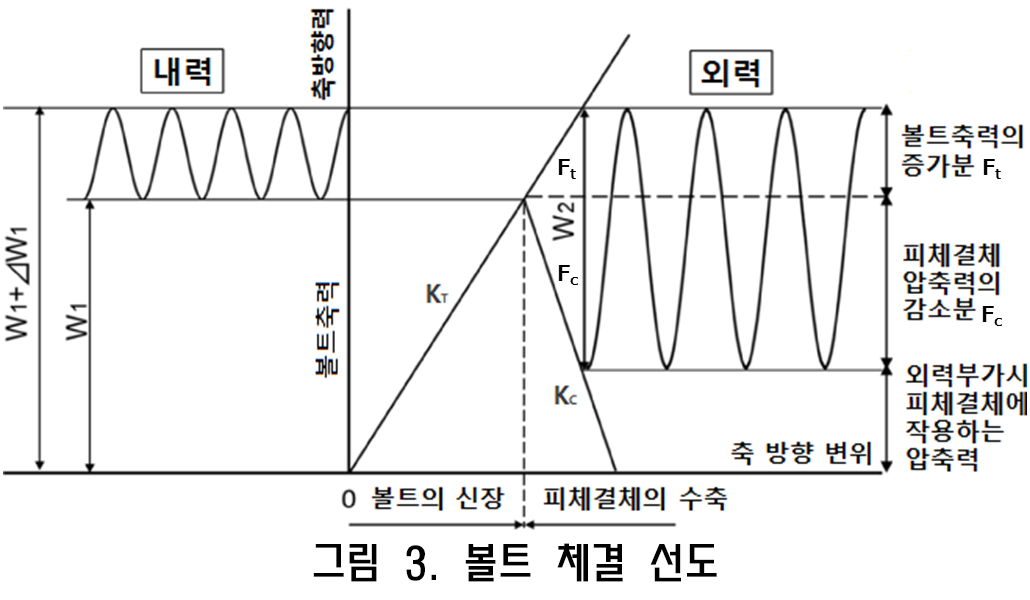

그림 3은 Ft , Fc , Kt , Kc를 이용하여 선도로 나타내고 있습니다. Kt와 Kc의 선이 교류하는 점이 초기축력Ff로 표시합니다. 또한 가로 축은 볼트 인장 (Kt) 및 피 체결부재 압축 (Kc)로 나타냅니다.
그러나 용수철 정수Kc를 어떻게 구할지가 문제입니다. 실험적으로 좌면을 볼수 없기에 변위를 정확히 측정할수가 없는것이 원인이라 추정식으로 많이 제안됩니다.
1960년대쯤 Thum&Debus의 식을 이용해서 얻은 내력 계수가 실험 측정값과 많이 다르다는 것을 판명되었습니다.
볼트 설계 예문

예문
2개의 원통을 체결하는 M나사 보통나사 볼트의 유효경을 정하시오. 단, 볼트의 강도구분은 8.8을 사용.
외력 W = 10000N
1) 원통의 외경 D는 D = 100mm, 내경 dh는 결정하는 볼트 유효경 d에 대하여 dh = d + 2(mm)로 함.
2) 외력 작용 시 원통 접합명에 잔류하는 응력σc가 σc = 10MPa이 됨.
해답
1) 외력 작용 시 접합면에 잔류하는 힘은 Ff – Fc가 됩니다. 앞서 말씀드렸듯이, 잔류하는 힘이 남아 있다는 전제하에 볼트 유효경을 구해야 하기 때문에 이와 같은 식을 이용합니다. Fc의 수치는 Fc = 0.9W, Ft = 0.1W으로 가정해도 좋습니다.
2) 게다가 볼트 초기 축력 Ff = 0.9σy(생략)입니다. 볼트 항복 응력σy는 볼트 강도구분 8.8이며 σy = 800 × 0.8 = 640MPa입니다.
3) 그러면, 볼트 초기 축력 Ff = 0.9σy × As = 576MPa × As. 또한 As는 볼트 나사부 유효 단면적(= π / 4 × ds2)으로 외력 작용 시 접합면에 잔류하는 힘은 Ff – Fc = 576 × As – 0.9W입니다.
4) 제1근사치로서, 유효 단면적은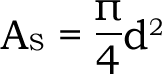 로 하고 유효경d를 이용합니다.
로 하고 유효경d를 이용합니다.
5) 접합면으로 힘의 균형을 생각하면 다음 식을 얻을 수 있습니다.
6) 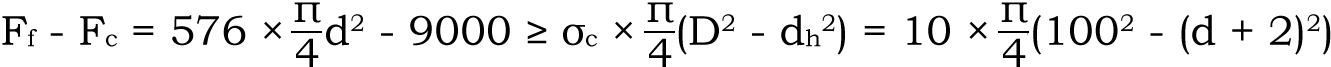 6)
6) 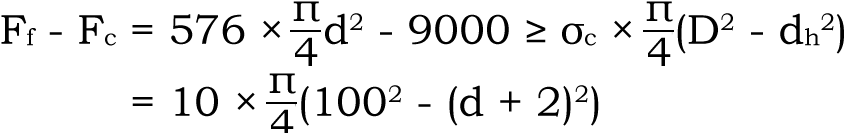
7) 위의 식을 풀면 d의 값은 d = 13.8mm가 된다. 따라서 볼트 유효경 후보로서는 M14와 M16이 적합합니다.
8) 다음 항목을 체크합니다. [ d2 : 유효경, As : 유효단면적, P : 피치, DB : 볼트머리 외경 ]
표 1. 각 사이즈별 주요 수치
| 호칭경 | d2(mm) | As(mm) | P(mm) | DB(mm) |
|---|---|---|---|---|
| M10 | 9.026 | 58.0 | 1.5 | 16 |
| M12 | 10.863 | 84.3 | 1.75 | 18 |
| (M14) | 12.701 | 115 | 2 | 21 |
| M16 | 14.701 | 157 | 2 | 24 |
| M20 | 18.376 | 245 | 2.5 | 30 |
| M24 | 22.051 | 353 | 3 | 36 |
9) M14의 주요 수치를 6)의 공식에 대입하여 비교하게 되면, Ff – Fc = 576 × As – 9000 = 57240N이 되고,
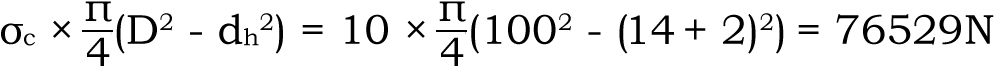 됩니다.
됩니다.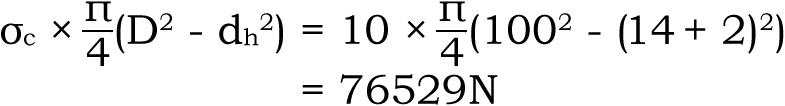 됩니다.
됩니다.
따라서 M14의 경우는 파손되기 쉬운 조건입니다.
다음으로 M16의 주요 수치를 6) 공식에 대입하여 비교하면 문제없다는 것 확인할 수 있으며, 결과적으로 M16의 볼트를 선택해야합니다.
10) 따라서 위와 같은 결과를 토대로 M16의 볼트를 선택하는 것이 좋습니다.
(부록) 플랜지 체결체의 강도설계에 필요한 다른 요인
볼트 강도구분이 커질수록 볼트 초기 체결력을 크게 취하는 것을 권장합니다.
이때의 중대한 문제점은 큰 체결력에 따른 볼트 너트 좌면의 꺼짐 혹은 함몰입니다.
따라서 아래의 항목을 고려하여야 합니다.
(1) 좌면강도
볼트 머리부 혹은 너트 좌면에 면압 즉, 단위 면적당 축력이 크면 초기 체결에 의해서 표면이 좌면에 접한 부분에 함몰되고, 사용중에 소성 변형이 진행되어 체결력 저하를 초래합니다.
이런 이유로 볼트에 발생하는 최대 하중에서 얻은 면압이 한계 면압을 넘지 않도록 설계할 필요가 있습니다. 식 (1-9)에 의해 얻은 초기 축력 이외 외력 W에 따른 볼트 축력 증가분은 Ft(=φW)이 됨으로 좌면에 있어 최대 면압P는 다음과 같습니다.
| 식 (1 – 12) – – – – 식 (1 – 12) | 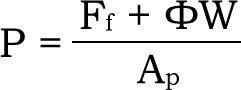 |
※Ap는 부하 좌면에 있어서 접촉 면적입니다. VDI2230(1)에 따른 한계 면압을 표시합니다.
(2) 꺼짐
볼트 체결부에 접촉면(나사면, 좌면, 접합면)에 있어서 거칢 등의 극부분적 소성변형은 체결 후 진행되지만, 외력작용에 따라서도 부분적으로 진행되는 경우도 있습니다.
이 꺼짐에 따른 축력저하 FZ를 정한 설계가 필요합니다.
꺼짐 량을 fZ라고 하면 FZ는 다음과 같은 식 (1-13)으로 얻을 수 있습니다. 그러나 상세한 연구가 필요합니다.
| 식 (1 – 13) – – – – 식 (1 – 13) | 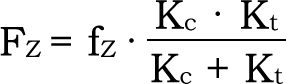 |
(3) 피로 강도
설계 포인트에 있어서 볼트의 피로 강도의 검증은 예를들어VDI2230에 따라 얻을수 있습니다.
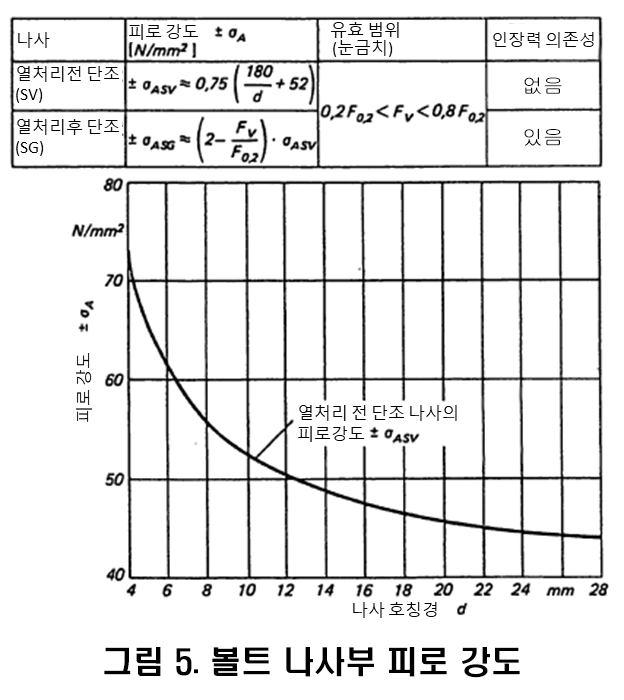

위 그림이 VDI2230으로 정해진 나사 유효경에 따른 강도의 그림입니다.
(4) 강도구분
볼트의 수치 결정으로는 강도와 항복 응력(내력)이 중요합니다. JIS나 KS에는 강도구분이 정해져 있습니다. 일반적으로 볼트의 체결시 및 외력 작용시에 볼트에 작용하는 등가 응력이 항복점(내력)을 넘지 않도록 설계합니다. 보통 강도구분이 큰 볼트를 높은 초기 축력으로 체결하는 것이 안전하다 라고 알려졌습니다.
예를 들면 강도구분 8.8은 처음 8이 인장강도로 800MPa을 나타내고, 항복 응력 혹은 내력이 800 × 0.8 = 640MPa이 됩니다.
(5) 체결
실제로 체결작업을 할 때는 초기 축력에 편차가 발생합니다.
αA를 αA = Ffmax / Ffmin이라고 하여, 체결 계수라고 하는 식이 있습니다. VDI2230에서 각종 체결법으로 αA값을 나타냅니다.
이 αA를 이용하여 볼트의 최대 초기 체결력 Ffmax를 나타내는 식은 아래의 식 (1-14)와 같습니다.
| 식 (1 – 14) – – – – 식 (1 – 14) | 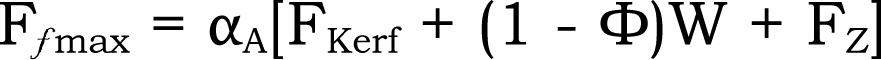 |
여기서FKerf는 누설 방지를 위한 압축력, FZ는 꺼짐에 의한 축력 저하입니다.
식 (1-12)의 기본적인 사고 방식은 볼트 축력의 편차를 인정하고 ① 적은 초기 체결력으로 체결하여도 최소 조건의 접합면 필요 최소 잔류량(가스켓 응력)을 만족시키고, ② 높은 체결력이라고 하더라도 볼트에서 발생하는 초기 축력(비틀림 포함)을 볼트 항복 응력의 90%이하로 체결하면 됩니다. 게다가 꺼짐에 의한 축력의 저하를 예상하고 그 저하축력을 미리 초기 축력에 추가해 두는 것입니다. 위와 같은 이유로 추가 조임은 필요 없게 되며, 합리적인 계산이 됩니다. 다른 특징은 기계설계에서 이용되는 안전률에 대한 사고방식이 있습니다만, 이번 내용에서 다루지 않겠습니다.
※ 참고문헌
(1) VDI 2230 Blatt1 (1986) “Systematic Calculation of High Strength Screw Fastening – Cylindrical Single Bolt Fastening”, Japan Screw Research Association, Kazuo Maruyama, Shunyuki Shinjizawa
(2) Yukio Okumura, Masahiko Okumura, Toshiyuki Sawa, Kengo Kuwagi, “Analyzing the Elastic Finite Element Stress Distribution of the Seat Stress of Hexagon Bolt Fasteners with Flanges and Estimating the Permanent Deformation (Initial Tightening)” Japan Mechanical Society Paper A, Volume 76 No. 772, pp1603-1611


